Technical Information

What is a Radiant Barrier?

A radiant barrier is a highly reflective material—usually aluminum foil—used in building construction to reduce heat transfer and improve energy efficiency. It works by reflecting radiant energy instead of absorbing it, unlike traditional insulation.

In homes, they are commonly installed under roof decking, laid over attic floor insulation, or stapled to rafters to reduce summer heat gain. In commercial and industrial buildings, radiant barriers are often used in warehouses, metal buildings, and distribution centers where roof and wall surfaces are directly exposed to intense solar radiation. They’re also effective in retrofit projects, HVAC duct insulation, and under radiant floor systems. Because they function by reflecting radiant energy regardless of orientation, radiant barriers can be integrated into nearly any building envelope design to improve thermal performance and reduce cooling loads.

‏‏‎ ‎‏‏‎ ‎‏‏‎ ‎What is Radiant Energy?

Radiant energy is the energy carried by electromagnetic waves. This includes everything from visible light and infrared heat to radio waves, ultraviolet light, and X-rays.

In the context of heat and buildings, radiant energy usually refers to infrared radiation—the invisible waves of heat that move through space and transfer warmth from one object to another without needing physical contact or a medium (like air or water).

In simple terms:
Radiant energy is heat or light that travels in waves.

What is Reflectivity?

Reflectivity—also referred to as reflectance—is the measure of how much radiant energy (light or heat) a surface reflects compared to how much it receives. It is expressed as a ratio or percentage, with a value ranging between 0 and 1, or 0% to 100%. A reflectivity of 1.0 (or 100%) means all incident radiation is reflected, while a value of 0.0 means all of it is absorbed.

In simple terms:

Reflectivity is how “shiny” a surface is in the eyes of energy.

This concept is especially critical in thermal management, building science, aerospace, and optics, where controlling heat transfer is essential for efficiency, comfort, and safety.

Types of Reflectivity

Reflectivity depends on surface properties and wavelength of the incoming radiation. It’s not a fixed trait—it varies depending on:

Wavelength of the radiation
- Some materials may reflect visible light well but poorly reflect infrared radiation.
Angle of incidence
- Radiation striking a surface at shallow angles can reflect differently than radiation striking head-on.
Surface texture and color
- Smooth, metallic surfaces are typically highly reflective.
- Dark, rough surfaces absorb more and reflect less.

The Science Behind Reflectivity

Reflectivity is governed by the law of conservation of energy. When radiant energy hits a surface, it is either:

Reflected (ρ): Bounced back toward the source.
Absorbed (α): Taken in by the material, often raising its temperature.
Transmitted (τ): Passed through the material.

For opaque materials (like aluminum foil used in radiant barriers), transmission is negligible:

ρ+α=1

This equation tells us:

The more reflective a surface is, the less energy it absorbs.

In thermal science, emissivity (ε)—a material’s ability to emit radiation—is often considered equal to absorptivity:

ρ+ε≈1 (for opaque surfaces)

So if a radiant barrier has an emissivity of 0.05, it reflects 95% of radiant heat—making it extremely efficient at rejecting radiant energy.

Reflectivity vs. Emissivity: A Crucial Pair

While reflectivity describes how much energy is bounced off a surface, emissivity describes how much energy is radiated (or “given off”). For energy-saving systems like radiant barriers, high reflectivity and low emissivity is the ideal combination.

Property	Ideal Value	Purpose
Reflectivity	≥ 0.95	Reflects incoming radiant heat
Emissivity	≤ 0.05	Minimizes heat re-radiation

‏‏‎ ‎Thermal Radiation & Reflectivity

Most of the radiant heat in buildings is in the longwave infrared range (5–25 microns), emitted from roofs, attics, and walls. Radiant barriers are specifically engineered to reflect this radiation.

Reflectivity (ρ): Typically ≥ 0.95 (95% of radiant energy reflected)
Emissivity (ε): Typically ≤ 0.05 (only 5% absorbed and emitted)
Key Equation: Reflectivity + Absorptivity = 1

‏‏‎ ‎‏‏‎ ‎‏‏‎ ‎What is an Electromagnetic Wave?

An electromagnetic wave is a form of energy that travels through space as oscillating electric and magnetic fields. These fields are perpendicular to each other and to the direction the wave is moving—this is why it’s called a transverse wave.

You interact with electromagnetic waves every day—they include visible light, radio waves, microwaves, infrared (heat), ultraviolet, X-rays, and gamma rays. All of these make up what’s called the electromagnetic spectrum.

What is an Electromagnetic Wave in the Thermal Spectrum?

An electromagnetic wave in the thermal spectrum refers to a wave of infrared radiation (IR)—a type of electromagnetic wave that is primarily associated with heat. These waves are not visible to the human eye, but you can feel them as warmth.

They lie just beyond the red end of the visible light spectrum and are emitted by any object with a temperature above absolute zero (−273.15°C or 0 Kelvin). This includes:

The human body
Roofs and walls
Asphalt, insulation, windows
Any building material that’s been heated by the sun

Wavelength Range of the Thermal Spectrum

The thermal (infrared) portion of the electromagnetic spectrum typically falls in this range:

Region	Wavelength Range	Characteristics
Near IR	0.75 – 1.5 µm	Close to visible light, some heat
Mid IR	1.5 – 5 µm	Stronger radiant heat
Far IR (thermal)	5 – 25 µm	Dominant range for heat emission from warm objects (this is what radiant barriers reflect most)

Most thermal radiation from buildings is concentrated in the 8 to 15 micron range (far infrared), especially from roof surfaces and attics heated by the sun.

Where Do Thermal Electromagnetic Waves Come From?

All matter emits thermal radiation according to its temperature. This is described by Planck’s Law and Stefan–Boltzmann Law, which show that:

Hotter objects emit more radiation
The peak wavelength shifts to shorter values as temperature increases

Example:

A roof at 150°F (65°C) emits thermal IR waves centered around 10 microns
A cooler interior wall might emit waves around 12–15 microns

Wavelength-Based Reflectance

Radiant barriers are specifically engineered to control radiant heat transfer, which occurs predominantly in the form of infrared (IR) radiation. The effectiveness of a radiant barrier is not uniform across all wavelengths—it varies depending on the spectral properties of the material and the wavelength of the incident radiation.

Radiant barriers are most effective in the longwave IR spectrum, which is dominant in hot roofs and attics. Their reflectivity increases with wavelength:

Visible Light (0.4–0.7 µm): Reflectivity ~0.60–0.80
Shortwave IR (1–5 µm): Reflectivity >0.85
Longwave IR (5–25 µm): Reflectivity ≥0.95

‎‎‎‎‏‏‎ ‎Equations That Matter

Planck’s Law: Describes intensity of radiation by wavelength and temperature.

B(λ, T) = [2hc² / λ⁵] * [1 / (e^(hc / λkT) - 1)]

Stefan-Boltzmann Law: describes the intensity of the thermal radiation emitted by matter in terms of that matter’s temperature.
E = εσT⁴ — small ε values = large heat savings.

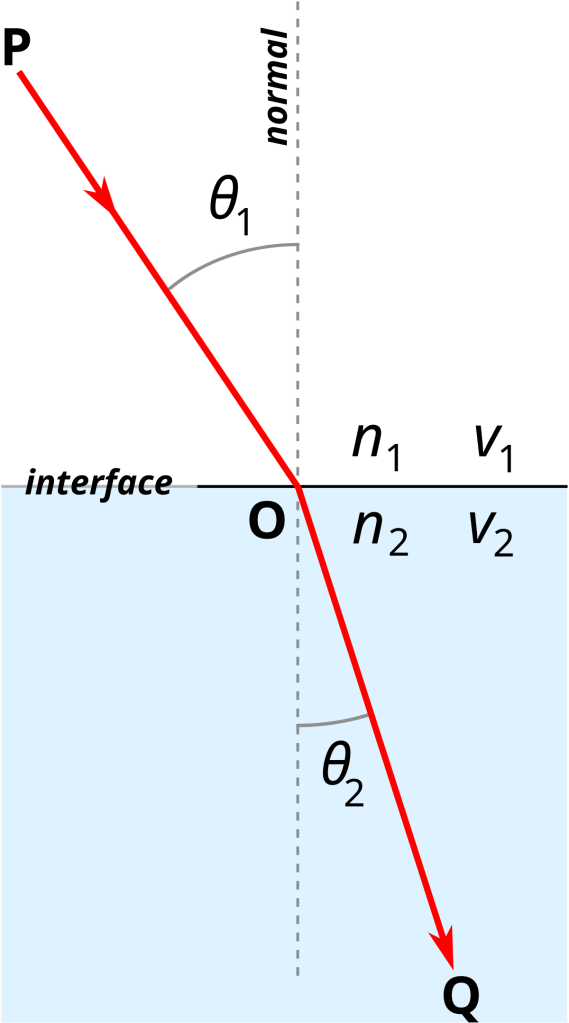
Snell’s Law – Refraction Direction: Although metals like aluminum don’t transmit light well (transmission is ~0), Snell’s Law helps define angles at interfaces:

n1 sinθ1 = n2 sinθ2

Where:

n1, n2 = refractive indices of air and aluminum
θ1 = angle of incidence
θ2 = angle of refraction (not really used with metals)

Fresnel Equations – Reflectance at an Interface: Fresnel equations define how much light is reflected vs transmitted at a boundary, depending on angle and polarization.

For unpolarized light (or average reflectance):
The reflectance (R) at a given angle θi is:

R(θ_i)= 1/2[|r_s/r_i|²+|r_p/r_i|²]

Example: Air to Aluminum in Thermal IR (~10 µm)

For thermal wavelengths (around 10 microns), aluminum has approximate optical constants:

n≈1.5n ≈ 1.5n≈1.5
k≈15k ≈ 15k≈15

Plugging these into the Fresnel equations, the reflectance at normal incidence is:

R=1+(1.5+i15) / 1−(1.5+i15)² ≈ 0.97

97% reflectance—which is why aluminum is ideal for radiant heat reflection.

Material Performance Comparison

Material	Reflectivity (5–20 µm)	Emissivity
Polished Aluminum	0.95–0.97	0.03–0.05
White Paint	0.20–0.25	0.85–0.90
Asphalt Roofing Felt	~0.10	~0.90

‏‏‎ ‎Practical Impact

A hot roof at 150°F emits ~600 W/m² of longwave IR. A radiant barrier with ε = 0.05 absorbs just 30 W/m² vs 540 W/m² absorbed by typical insulation. This leads to significant energy savings, lower cooling costs, and a more comfortable building envelope.

Conclusion

Radiant barriers are more than shiny foil—they’re science-based solutions engineered for peak performance in the thermal spectrum. Their high longwave reflectivity makes them essential for modern energy-efficient building design.